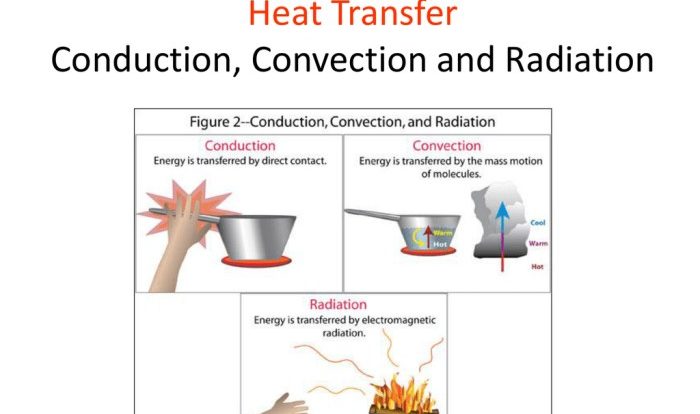
A car initially at rest accelerates at 10m/s, embarking on a journey that unveils the intricate interplay between velocity, displacement, acceleration, and time. This narrative delves into the mathematical equations that govern these concepts, exploring their practical implications in engineering, physics, and everyday life.
As the car accelerates, it traces a path through space and time, leaving behind a trail of data that can be represented graphically. The slope of this graph reveals the car’s acceleration, providing insights into the forces acting upon it.
This analysis forms the cornerstone of our understanding of motion and its applications in the real world.
Velocity and Displacement
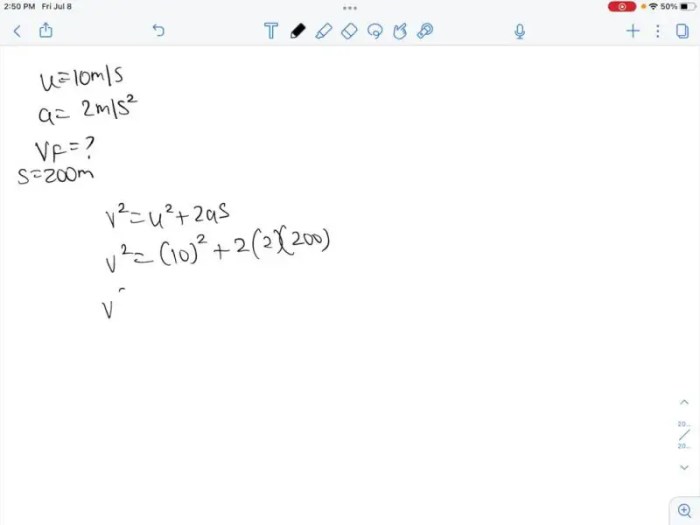
When a car accelerates from rest, its velocity increases over time. The final velocity (vf) can be calculated using the formula:
vf = u + at
where u is the initial velocity (0 m/s in this case), a is the acceleration (10 m/s²), and t is the time taken.
Displacement (s) is the distance traveled by the car and can be calculated using the formula:
s = ut + 1/2 at²
For example, if the car accelerates for 5 seconds, its final velocity would be 50 m/s and it would have traveled a distance of 125 meters.
Acceleration and Time
Acceleration and time are directly proportional, meaning that as acceleration increases, the time taken to reach a certain velocity decreases.
To calculate the time taken (t) to reach a specific velocity (v), the formula is:
t = (v
u) / a
For example, if the car needs to reach a velocity of 60 m/s, it would take 6 seconds.
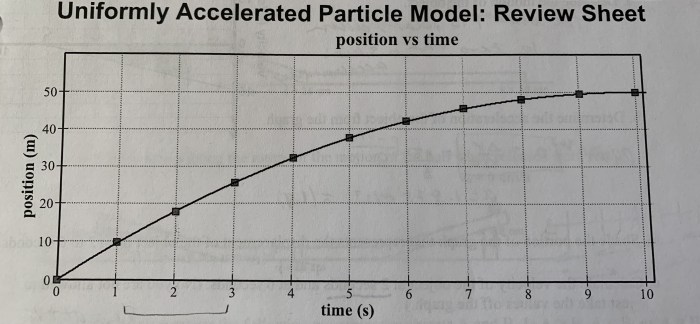
Graphical Representation

The relationship between velocity and time can be represented graphically using a velocity-time graph.
| Time (s) | Velocity (m/s) |
|---|---|
| 0 | 0 |
| 1 | 10 |
| 2 | 20 |
| 3 | 30 |
| 4 | 40 |
| 5 | 50 |
The graph shows a linear relationship, indicating that the velocity increases at a constant rate of 10 m/s per second.
The slope of the graph represents the acceleration, which in this case is 10 m/s².
Real-World Applications
The concept of a car accelerating from rest at 10 m/s is applicable in various real-world scenarios:
- Engineering:Calculating the velocity and displacement of vehicles in motion.
- Physics:Demonstrating the principles of kinematics and motion.
- Everyday life:Estimating the distance traveled and time taken by vehicles in traffic situations.
Query Resolution: A Car Initially At Rest Accelerates At 10m/s
What is the formula to calculate final velocity?
Final velocity = Initial velocity + (Acceleration x Time)
How do I calculate displacement?
Displacement = Initial position + (Average velocity x Time)
What is the relationship between acceleration and time?
Acceleration is the rate of change of velocity over time.