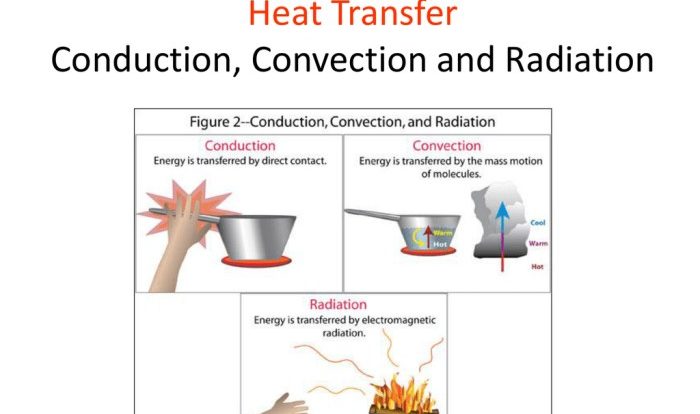
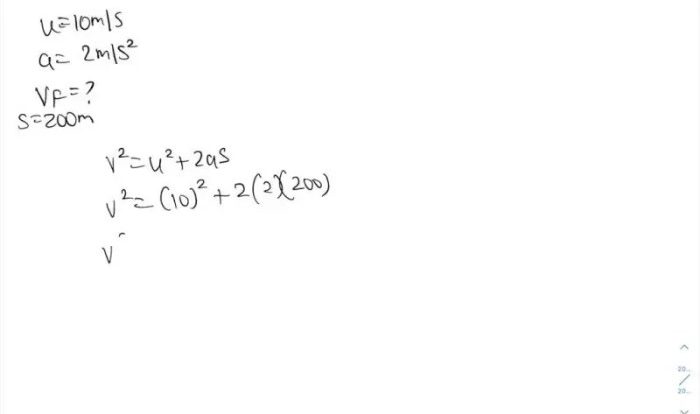The uniformly accelerated particle model review sheet provides a comprehensive overview of the fundamental concepts, applications, and limitations of this widely used model. It serves as an invaluable resource for students, researchers, and practitioners seeking to deepen their understanding of uniformly accelerated particle dynamics.
This review sheet delves into the core principles of uniform acceleration, exploring its mathematical foundations and practical implications. It examines the model’s assumptions and limitations, highlighting its applicability and potential pitfalls. Additionally, the sheet explores extensions and modifications made to the model, showcasing advancements in its accuracy and versatility.
Definitions
The uniformly accelerated particle model is a simplified model that describes the motion of a charged particle in a uniform electric or magnetic field.
Uniform acceleration refers to the constant rate at which the velocity of the particle changes.
Applications
The uniformly accelerated particle model is widely used in various fields, including:
- Particle accelerators
- Mass spectrometry
- Electron microscopy
Equations and Formulas
Key equations associated with the uniformly accelerated particle model include:
- Acceleration (a): a = qE/m (electric field) or a = qvB/m (magnetic field)
- Velocity (v): v = u + at
- Displacement (x): x = ut + 1/2at^2
These equations are derived from Newton’s second law (F = ma) and the definitions of acceleration, velocity, and displacement.
Assumptions and Limitations
The uniformly accelerated particle model assumes:
- The particle is point-like and has a constant charge.
- The electric or magnetic field is uniform and constant.
- The particle’s initial velocity is known.
Limitations of the model include:
- It does not account for relativistic effects.
- It does not apply to non-uniform fields.
- It does not consider the effects of collisions.
Extensions and Modifications
Extensions and modifications to the uniformly accelerated particle model have been made to improve its accuracy and applicability:
- Relativistic uniformly accelerated particle model: Considers relativistic effects.
- Monte Carlo model: Simulates particle trajectories in non-uniform fields.
- Molecular dynamics model: Considers the effects of collisions.
Comparison with Other Models: Uniformly Accelerated Particle Model Review Sheet
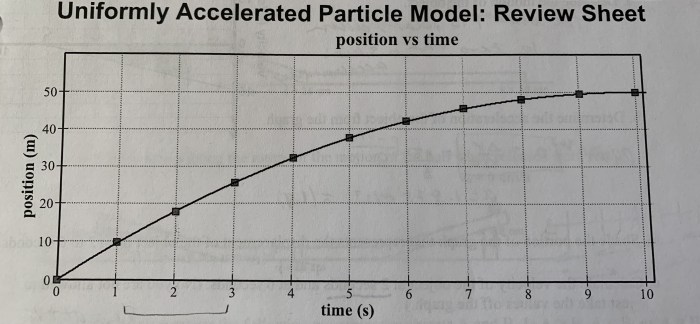
The uniformly accelerated particle model is similar to other models used to describe particle motion, such as:
- Constant velocity model: Assumes constant velocity.
- Projectile motion model: Considers the effects of gravity.
- Brownian motion model: Describes the random motion of particles in a fluid.
The uniformly accelerated particle model differs from these models in that it assumes constant acceleration due to an electric or magnetic field.
Experimental Verification
The uniformly accelerated particle model has been experimentally verified through:
- Cathode ray experiments: Demonstrated the deflection of electrons in an electric field.
- Cyclotron experiments: Verified the acceleration of charged particles in a magnetic field.
Applications in Technology
The uniformly accelerated particle model has practical applications in technology, including:
- Particle accelerators: Use electric fields to accelerate particles to high energies.
- Mass spectrometers: Use magnetic fields to separate ions based on their mass-to-charge ratio.
- Electron microscopes: Use magnetic fields to focus electron beams to achieve high resolution.
Answers to Common Questions
What are the key assumptions of the uniformly accelerated particle model?
The model assumes constant acceleration, negligible air resistance, and a uniform gravitational field.
How is the uniformly accelerated particle model used in real-world applications?
It is used in projectile motion calculations, spacecraft trajectory design, and particle accelerator simulations.
What are the limitations of the uniformly accelerated particle model?
It does not account for relativistic effects, air resistance, or non-uniform gravitational fields.